▼CS622:   Theory of Formal Languages
►Homework 10
On this page:
1 CS420 is Undecidable?
2 Closed Operations and TMs?
3 One more Undecidable Problem
4 Decidable vs Recognizable
    contents  ← prev  up  next → 

Homework 10

Last updated: Sun, 28 Apr 2024 00:19:02 -0400

Out: Mon Apr 24, 12:00pm EST (noon) Due: Wed May 01, 12:00pm EST (noon)

This assignment continues explore decidability, and also begins to look at undecidability.

Homework Problems

  1. CS420 is Undecidable? (12 points)

  2. Closed Operations and TMs? (8 + 8 = 16)

  3. One more Undecidable Problem (12 points)

  4. Decidable vs Recognizable (8 + 8 = 16)

  5. README (2 points)

Total: 58 points

Submitting

Submit your solution to this assignment in Gradescope hw10. Please assign each page to the correct problem and make sure your solutions are legible.

A submission must also include a README containing the required information.

1 CS420 is Undecidable?

Prove that the following language is undecidable:

\textit{CS420} = \left\{\left\langle M\right\rangle\mid M\textrm{ is a \textsf{TM} where }\texttt{CS420}\in L(M)\right\}

Your proof should be a proof by contradiction and should reduce from HALT_\textsf{TM}. It should also use the "modify the TM" technique from class.

If your proof creates a decider, it must include all required parts, including termination argument.

If your proof includes a statement like "Decider ABC decides language XYZ" then that statement needs to be justified with an example table that fully explains the (expected and actual) behavior of the machine. The table should also include the behavior of other TMs used to construct the decider.

2 Closed Operations and TMs?

Consider the following set operation on languages:

\mathit{BOTH}(A,B)=\left\{w\mid w\in A,w\in B\right\}

  1. Prove that the set of Decidable Languages is closed under \mathit{BOTH}.

  2. Prove that the set of Turing-Recognizable Languages is closed under \mathit{BOTH}.

For both of the parts above:

  • Come up with the proper and precise mathematical statement to prove first! Ask on Piazza if you are unsure. If you don’t do this, then the rest of the proof will be more difficult and likely incorrect.

  • If your proof includes a statement like "Decider ABC decides language XYZ" then that statement needs to be justified with an example table that fully explains the (expected and actual) behavior of the machine. The table should also include the behavior of other TMs used to construct the decider.

  • In particular, be careful with TMs that may loop. You should carefully explain why your solution properly handles these cases.

3 One more Undecidable Problem

Now let’s go the other way. Re-prove that EQ_\textsf{TM} is undecidable.

Your proof must reduce from the undecidable \textit{CS420} language from the CS420 is Undecidable? problem. (You may assume that the \textit{CS420} language is undecidable, even if you were unable to answer the earlier questions.) The proof must be a proof by contradiction.

If your proof creates a decider, it must include all required parts, including termination argument.

If your proof includes a statement like "Decider ABC decides language XYZ" then that statement needs to be justified with an example table that fully explains the (expected and actual) behavior of the machine. The table should also include the behavior of other TMs used to construct the decider.

4 Decidable vs Recognizable

Here’s our favorite diagram of languages again.

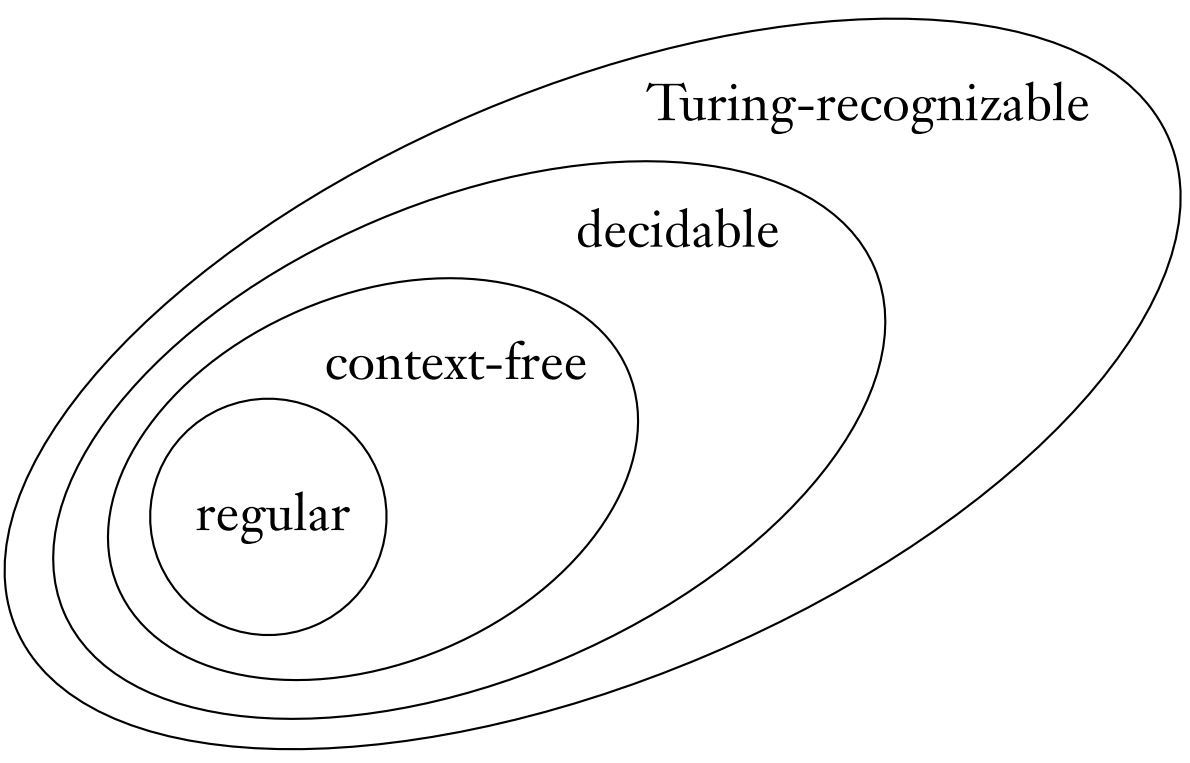
Prove that the outer two ovals are "correct". In other words:

  1. Prove that the decidable oval is a subset of the Turing-recognizable one.

  2. Prove that the Turing-recognizable oval is bigger than the decidable one.

For both of the parts above, come up with the proper and precise mathematical statement to prove first! Ask on Piazza if you are unsure. If you don’t do this, then the rest of the proof will be more difficult and likely incorrect.

    contents  ← prev  up  next →