Homework 2

Last updated: Mon, 31 Oct 2022 11:51:16 -0400

Out: Mon Sep 26, 00:00 EST Due: Sun Oct 02, 23:59 EST

This assignment explores nondeterministic finite automata (NFAs) and combining automata.

Homework Problems

1. NFA Formal Description (5 + 5 = 10 points)

2. DFAs vs NFAs (4 + 2 + 5 = 11 points)

3. Proving a Closed Operation For Regular Languages (8 points)

4. README (1 point)

Total: 30 points

Submitting

Submit your solution to this assignment in Gradescope hw2. Please assign each page to the correct problem and make sure your solutions are legible.

A submission must also include a README containing the required information.

1 NFA Formal Description

1. Recall that a NFA’s formal description has five components, e.g. N = (Q,\Sigma,\delta,q_{start},F), where \delta:Q\times\Sigma_\varepsilon\rightarrow\mathcal{P}(Q) is the transition function mapping a state and input symbol (or no symbol, in the case of an empty transition) to a set of states.

   Come up with a formal description for the following NFA:

   

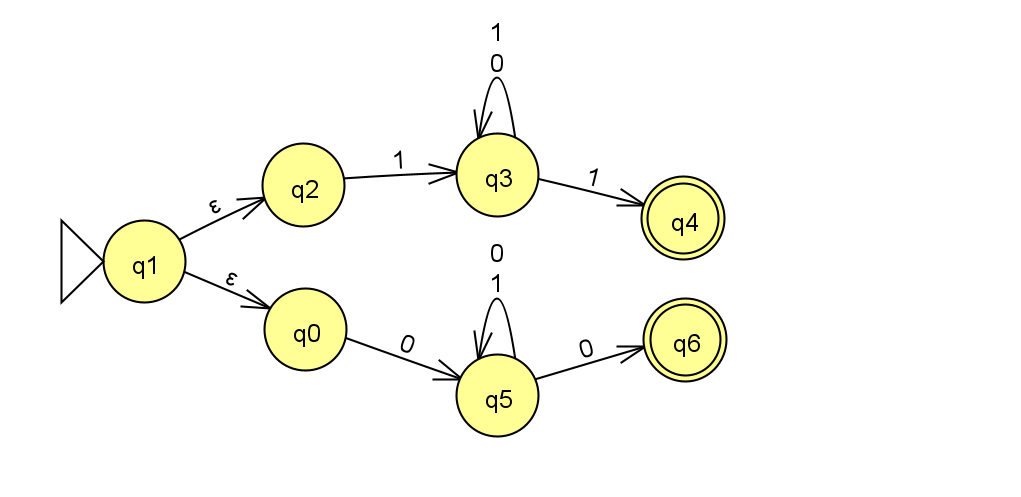
2. For each of following computations, say whether it represents an accepting computation or not. If so, give a possible sequence of states representing the accepting computation. If not, explain why:

   1. \hat{\delta}(q1,1001)

   2. \hat{\delta}(q2,1001)

   3. \hat{\delta}(q1,100)

   4. \hat{\delta}(q1,00)

   5. \hat{\delta}(q4,\varepsilon)

2 DFAs vs NFAs

1. Explain two possible differences between the formal description of a DFA and the formal description of an NFA.

2. Explain what it means for two machines to be equivalent.

3. Come up with a procedure \texttt{DFA}\!\!\rightarrow\!\!\texttt{NFA} that converts DFAs to equivalent NFAs.

   This means that given some DFA M = (Q,\Sigma,\delta,q_{start},F) that satisfies the formal definition of DFAs from class, \texttt{DFA}\!\!\rightarrow\!\!\texttt{NFA}(M) should produce some equivalent NFA N = (Q^\prime,\Sigma,\delta^\prime,q^\prime_{start},F^\prime) that satisfies the formal definition of NFAs.

3 Proving a Closed Operation For Regular Languages

Define the following operation, called \mathrm{OP}, on languages:

\mathrm{OP}(B,C)=\{x\mid x\notin B\textrm{ or }x \notin C\}

Prove that \mathrm{OP} is closed for regular languages.

Make sure your answer is in the form of a "Statements and Justifications" table, as explained in lecture (and also Hopcroft Chapter 1).